A Universal Image Quality Index (IC/UFAL)
Michel Alves (IC/UFAL)
Resumo: Apresentaremos o trabalho intitulado 'A Universal Image Quality Index' de autoria dos pesquisadores Zhou Wang e Alan C. Bovik. Neste trabalho é introduzido um novo índice para medição da qualidade de imagens, o UIQI. Movidos pela necessidade de uma métrica que fosse fácil de se obter e de ser empregada em várias aplicações de processamento de imagens, Zhou Wang e Alan Bovik propuseram um novo índice para mensuração da qualidade em imagens que diferente dos métodos tradicionais de somatório de erros, fosse concebido para modelagem de quaisquer distorções em imagens como uma combinação de três fatores: perda de correlação, distorções em luminosidade e distorções em contraste. Embora o novo índice possua baixa complexidade computacional, seja matematicamente definido, modelado para lidar com diferentes tipos de distorções e sem emprego explícito de um sistema de avaliação visual humana, experiências com vários tipos de distorções em imagens mostram que o mesmo exibe uma surpreendente consistência em relação a medição da qualidade subjetiva, possuindo uma performance significativamente melhor que o amplamente utilizado erro médio quadrático. O índice pode ser visualizado diretamente abaixo: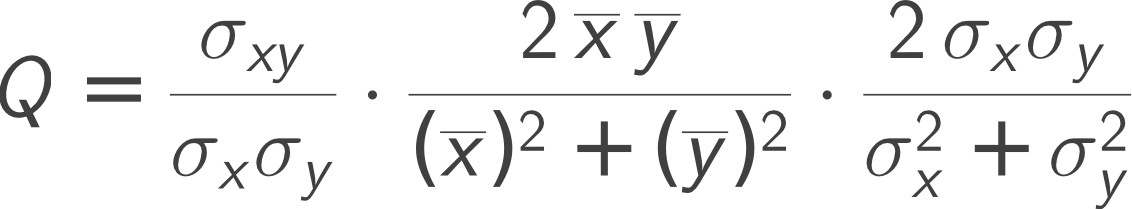
Dia: 07 de abril de 2011 (Quinta-feira)
Horário: 15h e 30 min
Local: Laboratório de Computação Gráfica
Hipersuperfícies com Curvatura Média Constante e Hipersuperfícies com Curvatura Escalar Constante na Esfera
Isadora Maria de Jesus (IM/UFAL)
Resumo: Nesta palestra, demonstraremos um teorema de Alencar e Do Carmo que caracteriza as hipersuperfícies com curvatura média constante na esfera (n+1)-dimensional. Utilizaremos esta caracterização para provar o Teorema de Li Haizhong para hipersuperfícies com curvatura escalar constante na esfera (n+1)-dimensional.
Dia: 18 de junho de 2009 (Quinta-feira)
Horário: 15h e 30 min
Local: Sala da Pós-Graduação em Matemática
O Teorema de Alexandrov
Gregório Manoel da Silva Neto (IM/UFAL)
Resumo: o Teorema de Alexandrov foi provado, originalmente, por A. D. Alexandrov em 1962, e estabelece que as únicas hipersuperfícies compactas, conexas e mergulhadas no espaço Euclidiano com curvatura média constante são as esferas. A demonstração dada aqui segue as idéias de Robert Reilly no seu artigo “Applications of the Hessian Operator in a Riemannian Manifold” publicado no “Indianna University Mathematical journal” nº 23, 1997, páginas 459-472, e usa técnicas de Análise Geométrica. Mais especificamente ele obteve uma versão integral da fórmula de Bochner. Além disso, provamos um teorema de comparação devido a Bishop, além de algumas de suas importantes implicações, a saber, as estimativas do volume de bolas geodésicas de Bishop e Yau, o Teorema de Bonnet-Myers e o teorema de Cheng.
Dia: 04 de junho de 2009 (Quinta-feira)
Horário: 15h e 30 min
Local: Sala da Pós-Graduação em Matemática
Soluções globais de baixa regularidade para o sistema de Schrödinger-Debye
Professor Adán Corcho (UFAL)
Resumo: Provaremos a existência de soluções globais para o sistema dispersivo de Schrödinger-Debye em espaços de Sobolev fora do espaço de energia.
Dia: 15 de maio de 2009 (Sexta-feira)
Horário: 16h
Local: Sala de Seminários no Instituto de Física – UFAL
Contribuições ao 18° Problema de Hilbert via Teoria Algébrica dos Números e Equações Diofantinas Clássicas
Professor André Flores (UFAL - Arapiraca)
Dia: 08 de maio
Horário: 10h e 30 min
Local: Sala da Pós-Graduação em Matemática IM/UFAL
O Teorema de Lindelöf para catenóides no R3 revisto
Professor Pierre Bérard (Université de Grenoble)
Resumo: Em 1870, Leonard Lindelöf publicou um artigo no segundo volume das Mathematische Annalen no qual ele estuda as propriedades de estabilidade do catenóide no R3. Nesta conferência daremos uma prova deste resultado e mostraremos como generaliza-la para estudar as propriedades de estabilidade dos catenóides no espaço H3 e no espaço H2 x R.
Dia: 28 de abril
Horário: 10h e 30 min
Local: Sala da Pós-Graduação em Matemática IM/UFAL


