Desenvolvimento de um Sistema para Conversão de Coberturas de Imagens Geo-Referrenciadas
Ailton Felix (IC/UFAL)
Resumo: A area de Sistemas de Informações Geográficas (SIG) envolve a modelagem, a visualização e o emprego de uma vasta gama de algoritmos para processamento de dados georreferenciados. As aplicações dessa natureza, de um modo geral, requerem um pré-processamento dos dados para que o uso dos mesmos seja viabilizado, pois esses dados exigem um alto custo computacional para armazenamento, acesso, tratamento e representação. O sistema sugerido aborda o problema de uma cobertura de imagens que possui segmentos diferentes que cobrem a mesma parte de uma região do globo terrestre, ou seja, as imagens apresentam uma sobreposição ou interseção de regiões, tendo assim uma redundância de informação e dificultando a manipulação dos dados por parte da aplicação. Além disso as imagens adquiridas possuem diferentes tamanhos, resoluções, posicionamentos e orientações. A essa cobertura damos o nomes de cobertura irregular com sobreposição. Será apresentado um método de conversão de cobertura de imagens, onde dado um conjunto de imagens de uma cobertura irregular com sobreposição serão geradas imagens que possuam as mesmas dimensões e estarão distribuídas em uma mesma estrutura de uma grade regular uniforme, teremos então como resultado uma cobertura regular uniforme.
Dia: 19 de maio de 2011 (Quinta-feira)
Horário: 15h e 30 min
Local: Laboratório de Computação Gráfica
Poligonização de Superfícies Implícitas
Adriano Barbosa (IM/UFAL)
Resumo: Dada uma função f:R3 -> R, o conjunto S = {(x, y, z) ∈ R3 | f(x, y, z) = c} onde c é um valor regular de f, é chamado superfície implícita. Superfícies implícitas são aplamante utilizadas em imagens médicas, modelagem molecular, CAD (Computer Aided Design), etc. Mas devido a sua natureza, superfícies implícitas são muito difíceis de se desenhar. Por outro lado, desenhar polígonos no computador é uma tarefa muito fácil. Apresentaremos um trabalho devido a T.Karkanis e A.J.Stewart, onde a superfície é triangulizada de tal modo que os triângulos da malha são bem próximos de triângulos equiláteros e que o tamanho de suas arestas depende da curvatura local da superfície. Como resultado teremos uma malha "bem comportada" com triângulos gordinhos, que implica em uma quantidade menor de triângulos, facilitando o desenho. Revisaremos alguns conceitos de Geometria Diferêncial e Análise como curvatura de superfície, triangulação e Teorema da função Implícita.
Dia: 12 de maio de 2011 (Quinta-feira)
Horário: 15h e 30 min
Local: Laboratório de Computação Gráfica
Learning good views through intelligent galleries
Thales Vieira (IM/UFAL
Resumo: The definition of a good view of a 3D scene is highly subjective and strongly depends on both the scene content and the 3D application. Usually,camera placement is performed directly by the user, and that task may be laborious. Existing automatic virtual cameras guide the user by optimizing a single rule, e.g. maximizing the visible silhouette or the projected area. However, the use of a static pre-defined rule may fail in respecting the user s subjective understanding of the scene. This work introduces intelligent design galleries, a learning approach for subjective problems such as the camera placement. The interaction of the user with a design gallery teaches a statistical learning machine. The trained machine can then imitate the user, either by pre-selecting good views or by automatically placing the camera. The learning process relies on a Support Vector Machines for classifying views from a collection of descriptors, ranging from 2D image quality to 3D features visibility. Experiments of the automatic camera placement demonstrate that the proposed technique is efficient and handles scenes with occlusion and high depth complexities. This work also includes user validations of the intelligent gallery interface.
Dia: 05 de maio de 2011 (Quinta-feira)
Horário: 15h e 30 min
Local: Laboratório de Computação Gráfica
A Universal Image Quality Index (IC/UFAL)
Michel Alves (IC/UFAL)
Resumo: Apresentaremos o trabalho intitulado 'A Universal Image Quality Index' de autoria dos pesquisadores Zhou Wang e Alan C. Bovik. Neste trabalho é introduzido um novo índice para medição da qualidade de imagens, o UIQI. Movidos pela necessidade de uma métrica que fosse fácil de se obter e de ser empregada em várias aplicações de processamento de imagens, Zhou Wang e Alan Bovik propuseram um novo índice para mensuração da qualidade em imagens que diferente dos métodos tradicionais de somatório de erros, fosse concebido para modelagem de quaisquer distorções em imagens como uma combinação de três fatores: perda de correlação, distorções em luminosidade e distorções em contraste. Embora o novo índice possua baixa complexidade computacional, seja matematicamente definido, modelado para lidar com diferentes tipos de distorções e sem emprego explícito de um sistema de avaliação visual humana, experiências com vários tipos de distorções em imagens mostram que o mesmo exibe uma surpreendente consistência em relação a medição da qualidade subjetiva, possuindo uma performance significativamente melhor que o amplamente utilizado erro médio quadrático. O índice pode ser visualizado diretamente abaixo: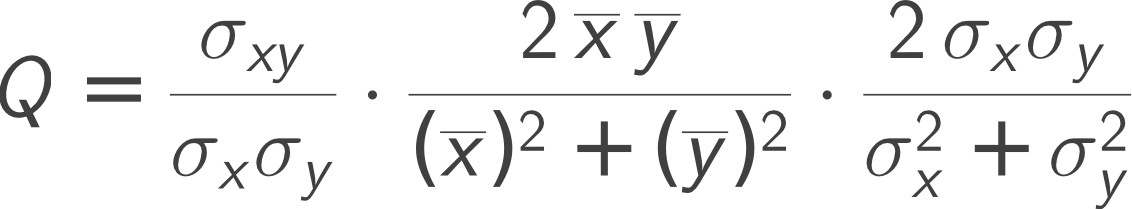
Dia: 07 de abril de 2011 (Quinta-feira)
Horário: 15h e 30 min
Local: Laboratório de Computação Gráfica
Hipersuperfícies com Curvatura Média Constante e Hipersuperfícies com Curvatura Escalar Constante na Esfera
Isadora Maria de Jesus (IM/UFAL)
Resumo: Nesta palestra, demonstraremos um teorema de Alencar e Do Carmo que caracteriza as hipersuperfícies com curvatura média constante na esfera (n+1)-dimensional. Utilizaremos esta caracterização para provar o Teorema de Li Haizhong para hipersuperfícies com curvatura escalar constante na esfera (n+1)-dimensional.
Dia: 18 de junho de 2009 (Quinta-feira)
Horário: 15h e 30 min
Local: Sala da Pós-Graduação em Matemática
O Teorema de Alexandrov
Gregório Manoel da Silva Neto (IM/UFAL)
Resumo: o Teorema de Alexandrov foi provado, originalmente, por A. D. Alexandrov em 1962, e estabelece que as únicas hipersuperfícies compactas, conexas e mergulhadas no espaço Euclidiano com curvatura média constante são as esferas. A demonstração dada aqui segue as idéias de Robert Reilly no seu artigo “Applications of the Hessian Operator in a Riemannian Manifold” publicado no “Indianna University Mathematical journal” nº 23, 1997, páginas 459-472, e usa técnicas de Análise Geométrica. Mais especificamente ele obteve uma versão integral da fórmula de Bochner. Além disso, provamos um teorema de comparação devido a Bishop, além de algumas de suas importantes implicações, a saber, as estimativas do volume de bolas geodésicas de Bishop e Yau, o Teorema de Bonnet-Myers e o teorema de Cheng.
Dia: 04 de junho de 2009 (Quinta-feira)
Horário: 15h e 30 min
Local: Sala da Pós-Graduação em Matemática


